Unraveling,Curvature,Journey,Through,Elegance,Calculus
The Enigmatic Curve: Unveiling Its Length Through Mathematical Prowess
In the realm of mathematics, curves captivate us with their intricate shapes, inviting us to explore their properties. Among these properties, the length of a curve stands as a fundamental measure, unlocking insights into its nature and behavior. However, determining this length is not always a straightforward task, often requiring ingenious mathematical techniques to unravel its secrets.
Calculating the length of a curve poses unique challenges due to its nonlinearity. Unlike straight lines, curves meander through space, introducing complexities that defy simple measurement. This intricate dance of curves demands specialized methods, blending calculus and geometry, to unravel their hidden dimensions.
The quest to calculate the length of a curve finds applications in diverse fields, ranging from engineering and physics to computer graphics and biology. In engineering, understanding the length of a curve is crucial for designing efficient structures and optimizing fluid flow. In physics, it aids in analyzing the motion of objects along curved trajectories. Computer graphics relies on curve length calculations to create realistic animations and models. And in biology, it helps scientists analyze the intricate patterns of DNA and other biological structures.
Overall, calculating the length of a curve is a fascinating mathematical endeavor that unveils the hidden dimensions of these enigmatic shapes. It finds practical applications in various fields, empowering engineers, physicists, computer scientists, and biologists with valuable insights into the world around us.
Embark on a Journey Through the Labyrinth of Curves: Delving into the Art of Length Calculation
In the realm of mathematics, curves possess an intrinsic beauty that lies not only in their intricate shapes but also in the challenge they present to our analytical minds. One of the most captivating aspects of curves is their length, a measure that quantifies their extent. Calculating the length of a curve is an art that requires a blend of mathematical prowess and a deep appreciation for the underlying geometry. In this exploration, we will embark on a journey through the winding paths of curves, unraveling the secrets behind their length calculation.
The Essence of Curves: A Tapestry of Infinite Variation
Curves, in their essence, are a departure from the rigid linearity of straight lines. They possess a fluidity and grace that captivates the senses, inviting us to trace their contours and marvel at their diversity. Whether it's the gentle arc of a rainbow, the spiraling elegance of a seashell, or the intricate patterns of fractals, curves are ubiquitous in the world around us.

The length of a curve is a fundamental property that quantifies its extent, providing a numerical measure of its winding path. It captures the essence of a curve's journey, encapsulating its twists, turns, and undulations. Understanding the length of a curve opens doors to a deeper appreciation of its geometric characteristics and its role in various mathematical applications.
Unveiling the Secrets of Length Calculation: A Mathematical Odyssey
Calculating the length of a curve is an intricate dance between mathematics and geometry. It requires a keen eye for patterns, a mastery of calculus, and an unwavering dedication to precision. As we embark on this mathematical odyssey, we will encounter various techniques that unravel the secrets of curve length calculation.

Calculus, with its arsenal of differentiation and integration, emerges as a beacon of hope in the labyrinth of curve length calculation. Through the fundamental theorem of calculus, we forge a connection between the rate of change and the total change, enabling us to unravel the length of curves with precision.
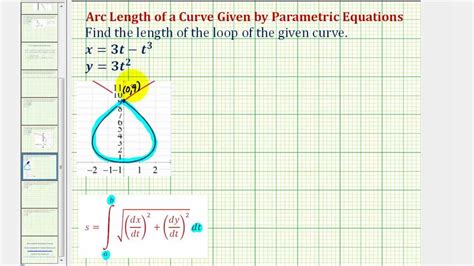
Parametric equations, with their ability to describe curves in terms of their coordinates, provide a powerful tool for length calculation. By unraveling the intricate dance of a curve's coordinates, we can piece together its overall length, much like connecting the dots in a intricate constellation.

When analytical methods falter, numerical methods step into the fray, providing a path to approximate the length of curves that defy exact calculation. These methods, such as the trapezoidal rule and Simpson's rule, wield their computational prowess to yield valuable estimates, bridging the gap between theory and reality.
The Symphony of Curves: A Chorus of Geometrical Intrigues
Curves, in their captivating diversity, present a symphony of geometrical intrigues. From the simplicity of the circle to the complexity of fractals, each curve possesses a unique story to tell, a tale of mathematical elegance and geometric harmony.
Circles, with their flawless symmetry and unwavering smoothness, stand as the epitome of geometric perfection. Their length, defined by the circumference, is a testament to their harmonious nature, representing the boundary of a perfectly enclosed space.

Ellipses, with their elongated charm, echo the grace of circles while introducing an element of eccentricity. Their length, captured by the formula involving the major and minor axes, unveils the subtle interplay between circularity and elongation.
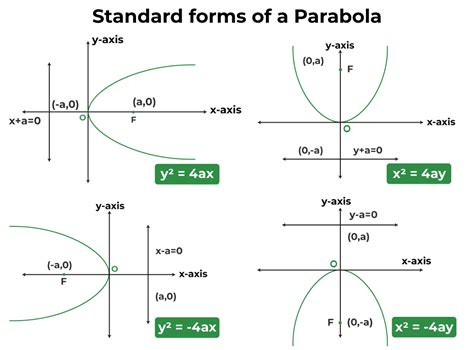
Parabolas, with their parabolic allure, present an intriguing case of asymmetry. Their length, determined through integration, reveals the intricate relationship between a point, a line, and the captivating shape that emerges from their interplay.
Conclusion: Length as a Gateway to Unveiling the Essence of Curves
The journey through the labyrinth of curves has unveiled the art of length calculation, showcasing its importance in quantifying the extent of these captivating mathematical entities. From the power of calculus to the elegance of parametric equations, we have explored the diverse techniques that unravel the secrets of curve length. As we bid farewell to this mathematical odyssey, let us carry with us the newfound appreciation for curves and their intrinsic beauty.
FAQs:
What is the significance of curve length in mathematics?
Curve length plays a crucial role in various mathematical applications, including geometry, physics, and engineering. It is used to measure the distance along a curve, calculate surface areas, and analyze the behavior of functions.
How does calculus contribute to curve length calculation?
Calculus provides a powerful framework for calculating the length of curves. Through the fundamental theorem of calculus, we can establish a connection between the rate of change and the total change, enabling us to determine the length of curves with precision.
What are parametric equations, and how are they used in curve length calculation?
Parametric equations are a method of representing curves by expressing their coordinates as functions of a parameter. They provide a convenient way to describe the motion of a point along a curve, which can be leveraged to calculate the length of the curve.
What numerical methods are commonly used for curve length calculation?
When analytical methods prove inadequate, numerical methods offer an alternative approach to approximating the length of curves. Techniques like the trapezoidal rule and Simpson's rule